Tyhle schody byste nevyšli: jak nám slavný matematik zamotal hlavu

Kam byste se po těchto schodech dostali? Zdroj: istockphoto.com

Některé optické klamy to dokonce dotáhly až do popkultury. Učitel Stephena Hawkinga se podílel na vytvoření několika zapeklitých hádanek, jež nám dodnes nedají spát.

Jméno Roger Penrose jste možná slyšeli. Jedná se o jednoho z nejslavnějších matematiků a fyziků 20. století, navíc byl i jakýmsi mentorem a spolupracovníkem jistého Stephena Hawkinga – a toho jste minout nemohli. Tento důstojný Brit navíc pocházel z intelektuálního zázemí, jeho otcem byl známý psychiatr a lékař Lionel Penrose. Otec se synem společně přišli i na několik optických klamů, které jste už také určitě viděli. Jenže víte, jak fungují?

Hrátky Rogera Penrose

Penroseovy schody jsou složitější variací staršího, ale podobně známého Penroseova trojúhelníku. Tomu se někdy říká také „tribar“ a patří mezi grafické paradoxy – tělesa, která by ve skutečném světě nemohla existovat. Jak je tedy možné, že je dokážeme nakreslit? Princip tohoto trojúhelníku totiž stojí na tom, že mezi všemi třemi trámy trojrozměrného trojúhelníku je úhel 90°; což však – jak si jistě pamatujete ze střední školy – není možné.

Penrose a optické klamy 2

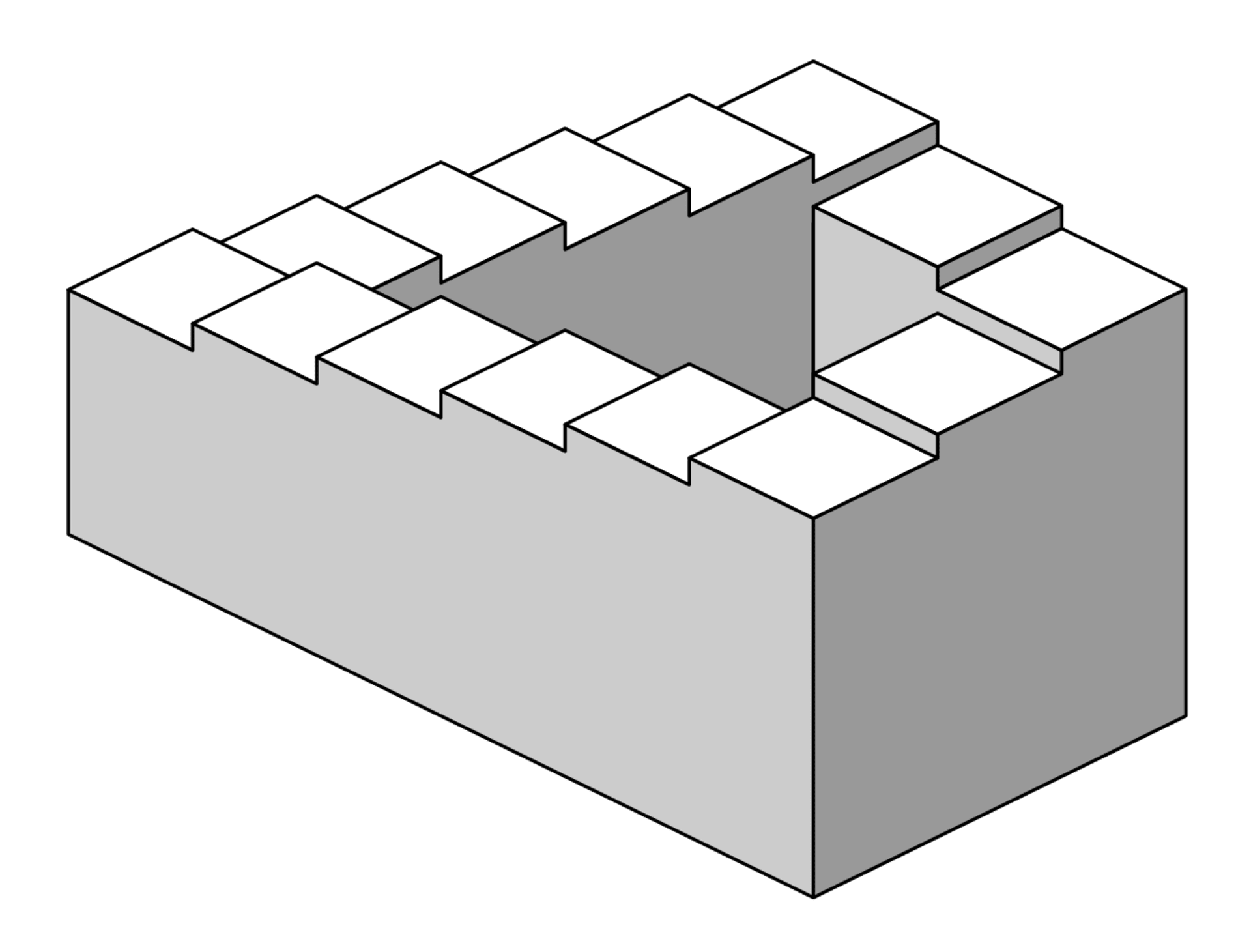
S tímto útvarem přišel už v 30. letech švédský umělec Oscar Reutersvärd, ovšem do všeobecného povědomí se zapsala až varianta Penroseů z 50. let. Tato „nemožnost v nejčistší formě“, jak trojúhelník sám Roger Penrose popsal, je pak podobná neméně slavné Möbiově pásce, pracující na stejném principu. A konečně se dostáváme i ke zmíněným schodům, v nichž každá ze čtyř částí struktury je sama o sobě reálná, ovšem dohromady vytvářejí nemožný objekt – soustavu schodů, která vede stále nahoru (nebo dolů, podle úhlu pohledu). Jak si ale takový úkaz vysvětlit?

Penrose a optické klamy 3

Nemožný trojúhelník i schody

Podle Penrose je odpověď právě v oné definující větě – chyba není v jednotlivých částech, nýbrž v jejich spojení dohromady. To navíc může proběhnout jen ve dvourozměrném prostoru (tedy na papíře či, jako v tomto případě, na displeji počítače či telefonu) a při snaze o převod struktury do skutečného, trojrozměrného prostoru se tento konstrukt zbortí. Což je vidět třeba na následujícím videu:

Není třeba dodávat, že nejsme jediní, koho tyto struktury fascinují. V umění i architektuře se staly inspirací pro mnoho tvůrců, jelikož i když víme, jak to funguje, náš mozek to pořád úplně nepobírá...

Text: MS