Koronavirus odhalil, že leckdo neví, co je to exponenciální růst

Dne 30. září napsal Deník N v rubrice Minutu po minutě, že byl v Česku podle ministra zdravotnictví Romana Prymuly od začátku září raketový nárůst případů koronaviru, který dosáhl exponenciálního charakteru. „Dostali jsme se na komunitní šíření, opatřeními z minulého týdne se podařilo exponenciální růst zastavit. Máme tady nárůst, ale při reprodukčním číslu 1,24, proto bylo nutné vyhlášení nouzového stavu,“ cituje deník ministra.

Číslo R (reprodukční) ve výpočtech majících pomoci modelovat vývoj pandemie říká, kolik lidí nakazí 1 člověk roznášející vir. Pokud by číslo R bylo rovno 2, první nakažený by dostal virus do 2 lidí, ti celkem do 4, následovala by řada 8, 16, 32, 64, 128… a epidemie by takto pokračovala až do doby, kdy by začali docházet lidé. To znamená situaci, kdy už by všichni byli nakažení, mrtví anebo by na ně virus nedosáhl (obyvatelé vzdálených ostrovů, od ostatních oddělené komunity atd.). Geometrická řada je jednoduchá, s exponenciálou je to složitější.

Dramatické grafy

Strmě stoupající počet nakažených, který atakuje hranici 10 000 osob za den, ukazuje, že se šíření viru zatím nedaří zastavit (článek je psán 16. října 2020). I vysocí politici používají argument: „kdybyste věděl, co je to exponenciální růst, nemohl byste tvrdit, že…“. Podívejme se proto co nejjednodušeji na to, co je to exponenciála a z ní odvozený růst.

Matematická funkce převedená do grafu

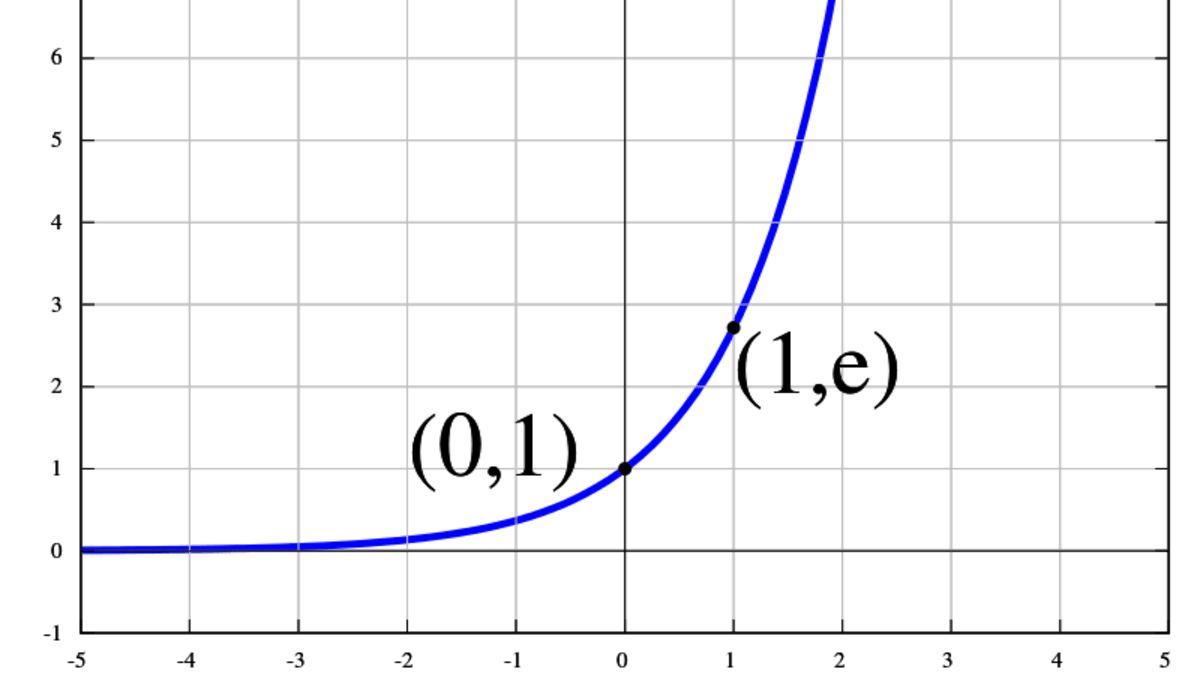
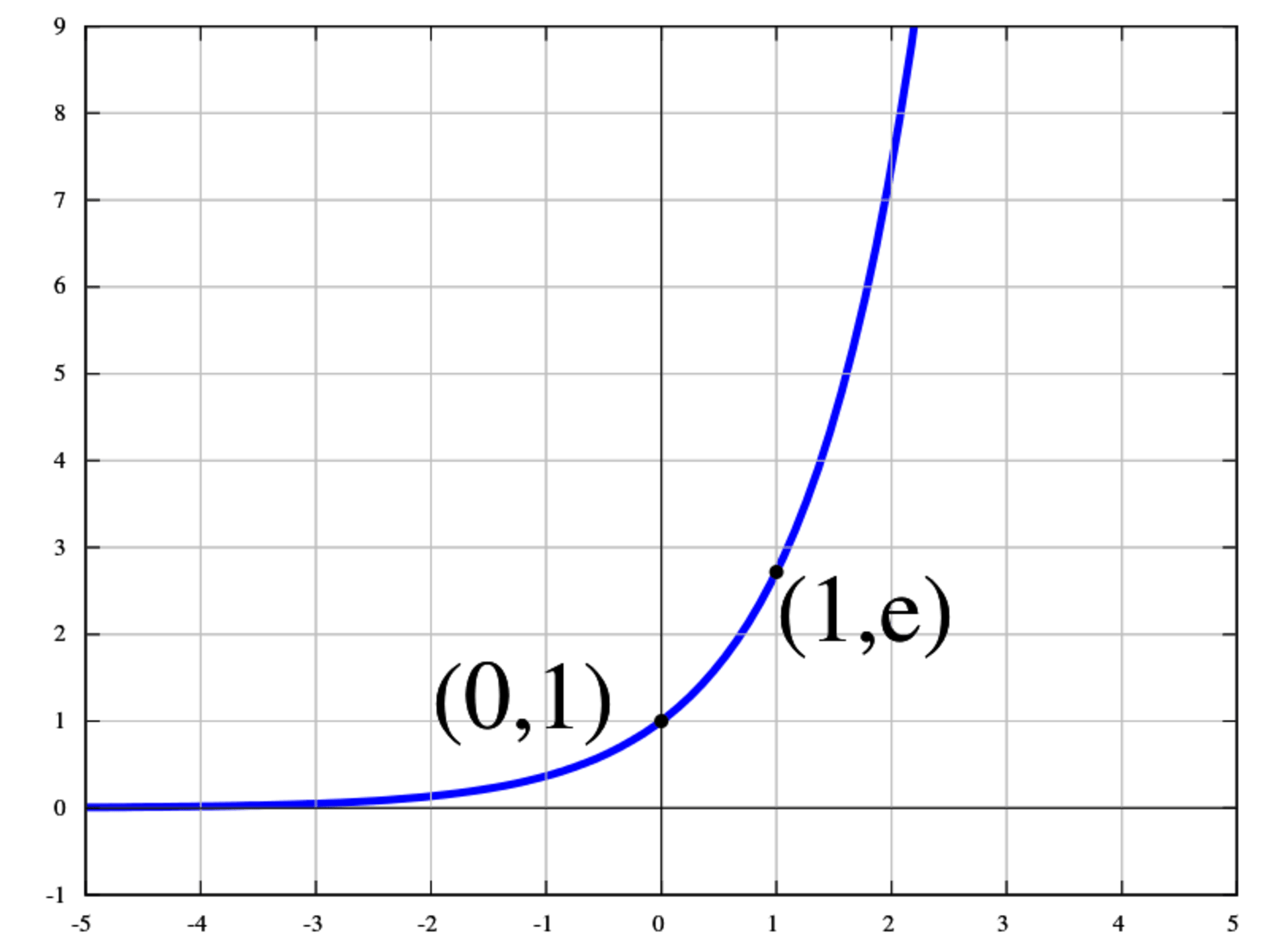
Zjednodušeně řečeno, exponenciální funkce (nikoliv exponenciála, k tomu se dostaneme na konci věty) je matematická funkce ve tvaru y = f(x) = ax, kde „a“ je kladné číslo jiné než 1 (tomu se říká základ), dále číslo „x“ se nazývá exponent a výsledným grafem je právě ona exponenciála. Množinou hodnot, které může exponenciální funkce nabývat, jsou všechna komplexní čísla. Matematici by bezesporu doplnili, že lze tuto jednoduchou definici rozšířit o další objekty, jako jsou například lineární operátory, ale to už se dostáváme mimo téma našeho článku. Obrácenou (inverzní) funkcí k exponenciále je mimochodem logaritmus se stejným základem.

Co je exponenciální růst

Tolik diskutovaná exponenciála je grafickým znázorněním exponenciální funkce. Jednoduše řečeno: exponenciála je graf. Exponenciální růst, o němž se tolik diskutuje v souvislosti s COVID-19, je matematický model růstu (například zvyšování počtu nakažených), který je vyjádřen pomocí exponenciální funkce času se základem vyšším než jedna.

V současné době se jednotliví odborníci mohou vášnivě přít, zdali se aktuálně jedná o exponenciální růst počtu nakažených či nikoliv, a navíc se čísla denně mění, takže včerejší výpočet už dnes vychází jinak. Nicméně stačí pohled na grafy, kterými nás denně média zásobují, a je jasné, že situace zatím skutečně roste takovým tempem, že se výpočet dá vyjádřit exponenciálou (grafem) a predikce vývoje vůbec není veselá. Modelování pandemií je přitom samozřejmě extrémně složité a závislé na extrémním množství proměnných. Číslo R, tedy množství lidí, které nakazí jeden přenašeč, je jen jedním (byť důležitým) faktorem.

Klíčové číslo R

Sami si pochopitelně můžete zkusit spočítat, jak takový exponenciální růst probíhá. Reprodukční číslo je totiž exponentem, a pokud si při R 1,6 dosadíte za základ třeba číslo 100 (tedy pokud by první den bylo 100 nakažených), druhý den bude nakažených 160 lidí. To nezní tak špatně, že? Vývoj dalších dnů by v takovém výpočtu byl 256 lidí, 409 lidí, 655 lidí... a pak začne exponenciála nabírat strmou křivku vzhůru a desátý den jsme na 6 872 nakažených.

Oproti tomu pokud by se R podařilo snížit na hodnotu 1,3 (což intuitivně oproti 1,6 nevypadá jako velký rozdíl), tak druhý den sice bude nakažených 130 (což není o moc méně), ale po deseti dnech místo 6 872 jen 1 060 – a to už je hodně velký rozdíl. I proto je podstatné snažit se snížit každou desetinu z hodnoty reprodukčního čísla, jinak si nekompromisní a neintuitivní exponenciální růst vybere vysokou daň.